leetcode Question 75: Recover Binary Search Tree

Recover Binary Search Tree

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Note:
A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

Analysis:

The question requires O(1) space, let's first consider the case without this.
How to traverse BST?
Yep! The inOrder tree traversal.  (left->root->right)
So the easiest way is inorder traverse the BST and find the element pair (two elements) which are not consistent with the definition of BST. In order to get the order, a queue is needed, which is O(n).

Now how to do this procedure in O(1)?
What we need is actually two pointers, which point to 2 tree nodes where is incorrect. Therefore, we only need to store these two pointers, and, we also need another pointer to store the previous element, in order to  compare if the current element is valid or not.

In the code below, you will find, the last step is to replace the wrong pair's value. And the inOrder function is to search the whole BST and find the wrong pairs.

Note that, (1)the previous element is NOT the root node of the current element, but the previous element in the "inOrder" order; (2) To store the wrong pair, the first found wrong element is stored in first pointer, while the next is stored in the second pointer.

e.g. The correct BST is below:

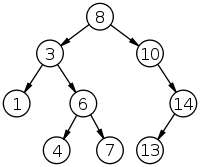
The inorder traversal is :  1 3 4 6 7 8 10 13 14

If we change the value 4 and 8:  1 3 8 6 7 4 10 13 14, when it goes to the node 6, now the pre->val = 8, check if pre<current node, which is wrong here (8>6). So we store the first pointer pointing to the node 6 and second pointer pointing to the node 8. To do so, we have stored the wrong nodes, if every other node keep the correct order, then swapping these nodes is enough for the problem. In other words, after the whole traversal, what we need to do is just changing the values of the first and second. Continue our example here, when the traversal goes to the node 4, now the node 7 is its pre, which is also wrong, so the second wrong node is found, and we change the second pointer pointing to node 4.

Code(C++):

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode *first;
    TreeNode *second;
    TreeNode *pre;
    
    void inOrder(TreeNode *root){
        if (root==NULL){return;}
        else{
            inOrder(root->left);
            if (pre == NULL){pre = root;}
            else {
                if (pre->val > root->val){
                    if (first==NULL) {first = pre;}
                    second = root;
                }
                pre = root;
            }
            inOrder(root->right);
            
        }
    }
    void recoverTree(TreeNode *root) {
        // Start typing your C/C++ solution below
        // DO NOT write int main() function
        pre = NULL;
        first = NULL;
        second= NULL;
        inOrder(root);
        int val;
        val = first->val;
        first->val=second->val;
        second->val=val;
        return;
    }
};

Code(Python):

# Definition for a  binary tree node
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    # @param root, a tree node
    # @return a tree node
    prev = None
    p1 = None
    p2 = None
    
    def inOrder(self, root):
        if root == None:
            return
        else:
            self.inOrder(root.left)
            if self.prev == None:
                self.prev = root
            else:
                if root.val <= self.prev.val:
                    if self.p1 == None:
                        self.p1 = self.prev
                    self.p2 = root
                self.prev = root
            self.inOrder(root.right)
    
    def recoverTree(self, root):
        self.prev = None
        self.p1 = None
        self.p2 = None
        self.inOrder(root)
        tmp = self.p1.val
        self.p1.val = self.p2.val
        self.p2.val = tmp
        return root