leetcode Question: Search a 2D Matrix II

Search a 2D Matrix II

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

For example,

Consider the following matrix:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, return false.

Analysis:

Since the matrix is sorted by column and row, we can easliy know that:

• matrix[ i ] [ j ]  <= matrix [ i-1 ] [ j ]
• matrix[ i ] [ j ]  >= matrix [ i ] [ j-1 ]

For the element in the top right (or bottom left), we could find out:

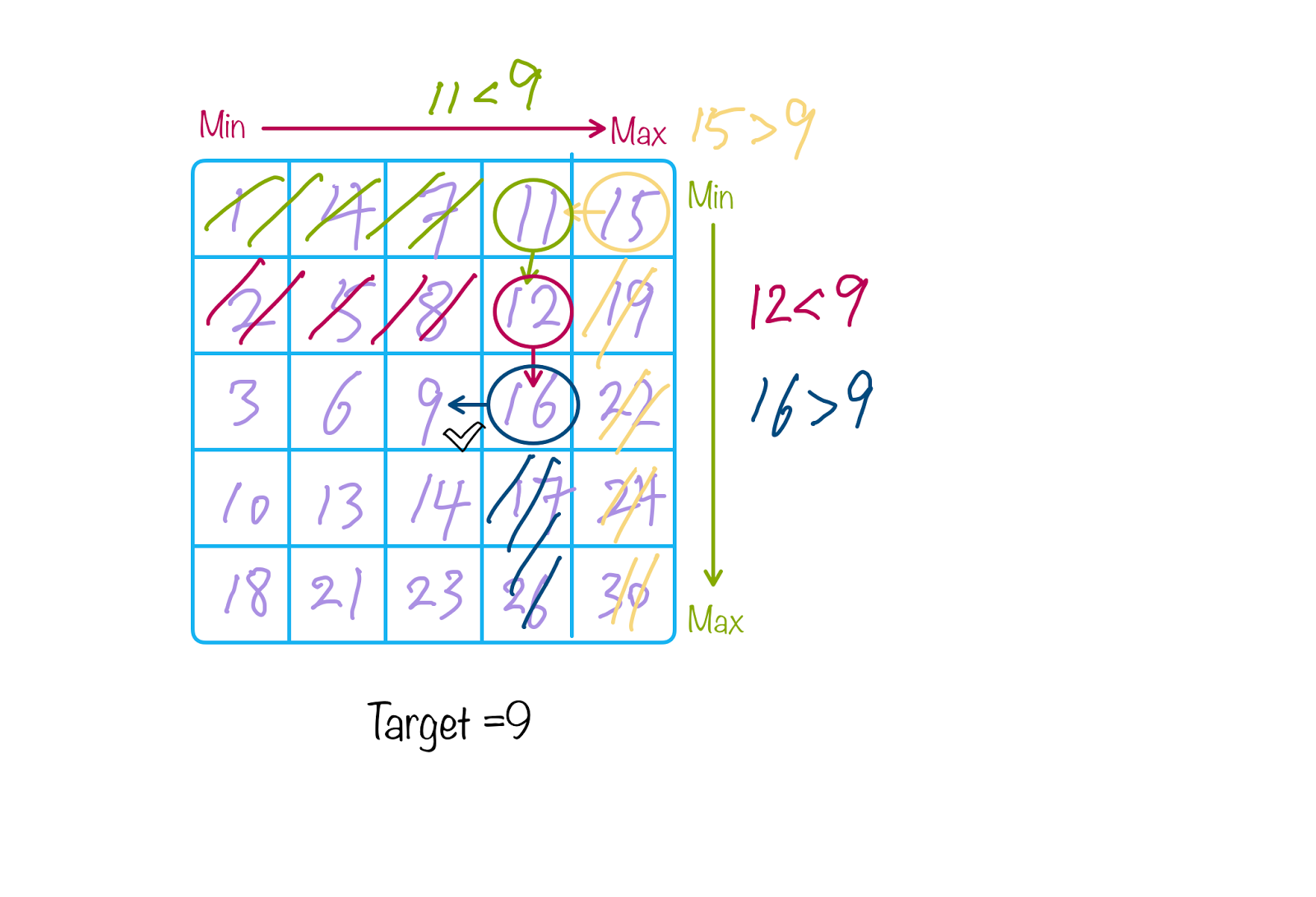
• if target < top right, then target cannot be in last column.  
• if target > top right, then target cannot be in the first row.

Therefore, search from the top right (or bottom left) with two pointers (for row and column), will eliminate either a row or a column in each iteration, the overall time complexity is O(m + n).

Code (C++): 

class Solution {

public:

bool searchMatrix(vector<vector<int>>& matrix, int target) {

int nRow = matrix.size();

if (nRow == 0) {return false;}

int nCol = matrix[0].size();

if (nCol == 0) {return false;}

int i = 0;

int j = nCol - 1;

while (i < nRow && j >=0){

if (matrix[i][j] < target){

i++;

}else if (matrix[i][j] > target){

j--;

}else{

return true;

}

}

return false;

}

};

Code (Python):

class Solution(object):

def searchMatrix(self, matrix, target):

"""

:type matrix: List[List[int]]

:type target: int

:rtype: bool

"""

i = 0

j = len(matrix[0]) -1

while i < len(matrix) and j >= 0:

if matrix[i][j] < target:

i += 1

elif matrix[i][j] > target:

j -= 1

else:

return True

return False