Range Sum Query 2D - Immutable
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Range Sum Query 2D
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
Note:
You may assume that the matrix does not change.
There are many calls to sumRegion function.
You may assume that row1 ≤ row2 and col1 ≤ col2.
Analysis
First glance at this problem give us an intuitive but less efficient solution: Loop through row1 to row2, loop through col1 to col2, add the matrix element one by one.
Given the condition that there are many function calls, we could start thinking of more efficient algorithm. Since the matrix does not change, we could possiblly store some information before the "sumRegion" calls, in order to help on the time complexity.
Firstly let's simplify the problem to the following description:
given a matrix, and one point, which is the bottom right corner, compute the sum of the region between (0, 0) and the point.
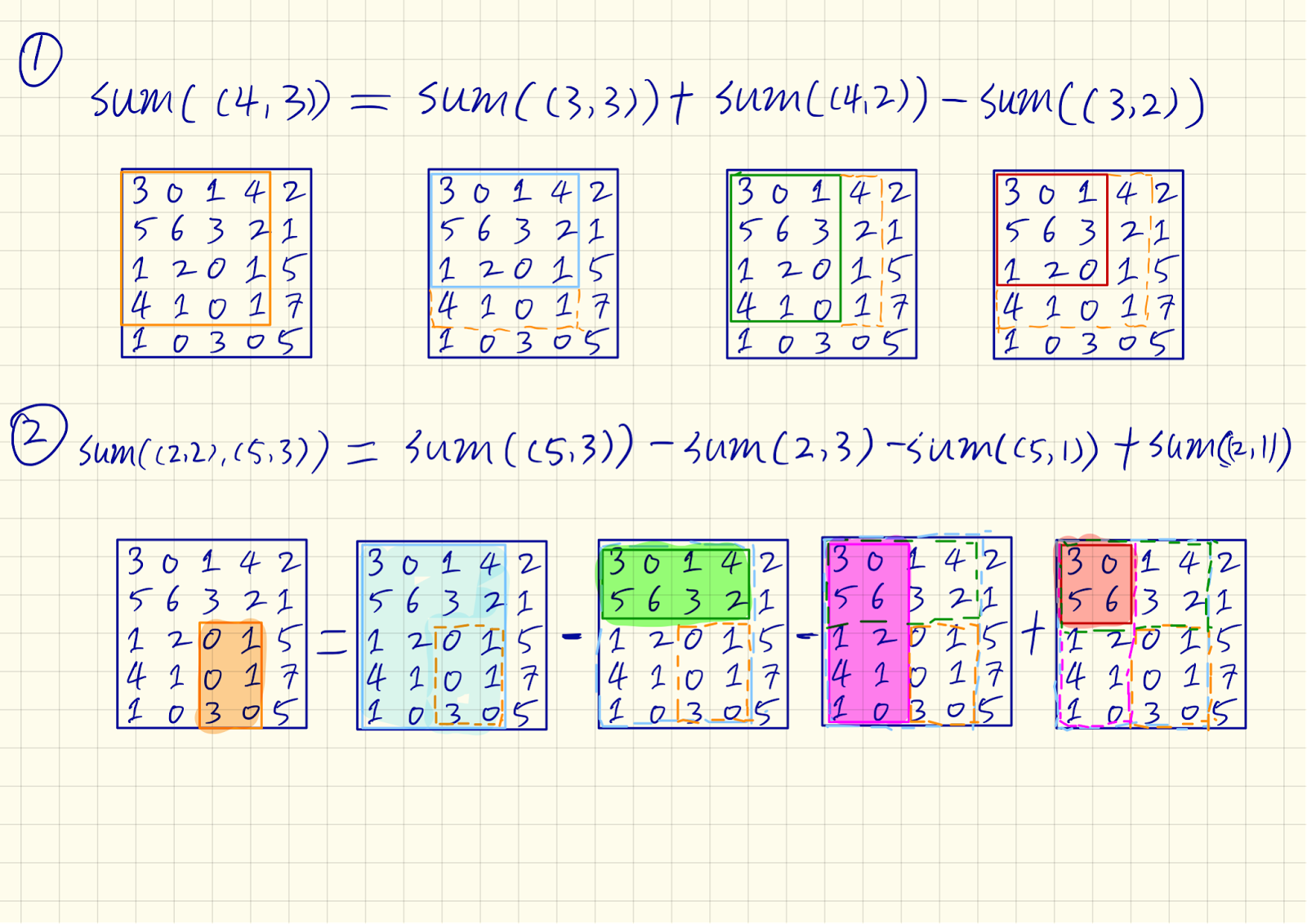
It's more intuitive to draw the figure below ( see (1) ):
From the figure, we could see the procedure to compute the sum of region by addition and subtraction.
Looking back to the original problem, it is then not hard to find out (figure (2) ):
sumRegion(row1, col1, row2, col2) = sum( (row2, col2) ) - sum( (row1-1, col2) ) - sum( (row2, col1-1) ) + sum( (row1-1, col1-1) )
Now, the only thing of which you may not get the idea is the initialization part. Actually it is not that hard but need more attention dealing with the indices. Specifically, we build a matrix of the same size, where every position [ i, j ] stores the sum of element between [0 , 0] and [ i, j ]. We are still using the procedure shown in figure (1):
For each position [ i, j ] in our sum matrix, we are checking [ i-1, j ] and [ i, j-1 ], the sum of [ i, j ] is:
m[ i, j ] = m[ i-1, j ] + m[ i, j-1 ] - m[ i-1, j-1 ], the procedure is shown below:

ReplyDeletecancel norton antivirus
how to cancel norton subscription
how to cancel a norton subscription
how to cancel norton antivirus subscription
how to cancel avast auto renewal
how to cancel norton subscription and get refund
norton antivirus cancellation refund
how to cancel norton
This comment has been removed by the author.
ReplyDeleteBuy Ghb online
ReplyDeleteBuy Gbl online